Bonjour à tous !

Merci d’être venus pour écouter une conférence de philosophie. Je vais vous parler d’un philosophe qui me tient à cœur, Gaston Bachelard.

On m’a demandé de réfléchir à la conception des ruptures en science selon Gaston Bachelard. C’est souvent l’un des éléments que l’on retient de son épistémologie, qui insiste sur la nécessité de ruptures, que l’on appelle parfois les ruptures épistémologiques. En son temps, cela représentait une vraie nouveauté.

Avant d’aborder le sujet, je vais vous présenter Gaston Bachelard. J’ai mis quelques dates principales de publication de ses ouvrages, notamment ceux que je vais citer au cours de mon exposé. Mais il est intéressant pour comprendre la trajectoire intellectuelle de Gaston Bachelard de rappeler aussi ce qu’a été sa vie.

Il est né en 1884, dans un village de Champagne qui est Bar-sur-Aube. Son père était cordonnier. Sa mère tenait un dépôt de tabac et journaux.

Souvent, je dis : 1884, c’est un an après 1883. Au-delà du truisme, c’est parce que 1883, c’est la mise en place d’un certain nombre de lois de Jules Ferry, sur l’enseignement public, laïc, gratuit et obligatoire. Cela va permettre l’ascension dans la société française, que l’on a appelée l’échelle républicaine, d’enfants issus des classes populaires, à travers l’enseignement, puis ensuite à travers le recrutement dans un certain nombre d’institutions, comme l’éducation nationale, le P et T, les Chemins de fer. C’est tout le mouvement de la IIIe République d’ascension méritocratique à travers le savoir dont Bachelard va être une figure exemplaire.

Il fait de très brillantes études dans son village, au Collège et au Lycée. Il va jusqu’au baccalauréat. À cette époque, il y a trois baccalauréats. Le plus prestigieux, qui fait la reproduction des élites, c’est le baccalauréat littéraire avec le grec et le latin. Il y a un deuxième baccalauréat pour la bourgeoisie, qui est le baccalauréat de médecine. Et enfin, il y a le baccalauréat qu’on va dire populaire, qui est celui qui fait des maths et des sciences naturelles. C’est celui-là que Bachelard va passer, autant par destination sociale que par goût.

Après, venant d’un milieu relativement modeste, il va prendre un emploi, c’est l’équivalent de nos surveillants d’aujourd’hui, il est répétiteur dans un lycée et prépare un concours de recrutement de la Fonction publique, qui sera celui des P et T. Il va le réussir et être nommé à Paris où il sera ambulateur. Ce n’est pas exactement un postier, c’est celui qui prend le courrier à partir du centre de tri et qui le distribue à l’endroit où le postier va le prendre pour faire sa tournée. Quand il est nommé à Paris, il en profite pour s’inscrire au cours du soir et continuer à se former en mathématiques, en astronomie, en chimie. Il va continuer ses études, et il obtiendra l’équivalent de 7 « capacités ».

Il va faire son service militaire dans les Dragons, période où il dira qu’il s’est ennuyé quand même. Ensuite, quand il revient, il se met à préparer un autre concours. Son ambition dans la vie c’est de devenir ingénieur des P et T. Il passe le concours et il est reçu troisième, mais cette année-là, au lieu d’avoir trois places il n’y a que deux places. Il n’est donc pas pris. Il obtient sa mise en disponibilité pour préparer à plein temps la prochaine édition, qui lieu en 1914.

En 1914, quand la guerre éclate, il ne bénéficie pas de la protection accordée aux fonctionnaires soutiens de famille qui sont en poste, il est appelé au front. Il se marie tout de suite avec une institutrice, d’un village juste à côté du sien, avec laquelle il s’est lié, puis il va au front. Il va passer trente-huit mois dans les tranchés. Son rôle, comme il était au P et T, si vous avez une idée dans les films du type qui porte un gros sac sur le dos et qui déroule un fil, qui fait une cible facile pour la ligne d’en face, c’est lui ! Il sera décoré parce qu’il aura notamment rétablie, dans la dernière semaine de la guerre, sous une pluie d’obus, pendant soixante-douze heures d’affilée, la communication entre les lignes. Il survie miraculeusement, heureusement pour lui et heureusement pour nous.

Et à quelque chose malheur est bon… La Guerre de 14-18, une énorme saignée dans la population française, plus d’un million de morts parmi les hommes français, et 75% de pertes chez les officiers. Or, Bachelard, parce que sa femme était tombée malade de la tuberculose, avait passé le concours de recrutement des officiers pendant la guerre, pour pouvoir avoir une meilleure paye et pourvoir compenser ses arrêts maladie. Il a survécu. 75% des officiers sont morts, et les officiers c’étaient très souvent des saint-cyriens, mais c’étaient aussi des normaliens, des polytechniciens. Autrement dit, toute l’intelligentsia française a été annihilée, balayée. Une génération entièrement saignée. Quand il revient de la guerre, il se présente au Ministère de l’éducation et il dit : moi, ce que j’aimerais faire, c’est enseigner. On lui dit : où, vous voulez. Il dit : je veux être prof dans mon village. On lui dit : pas de problème. Et on lui fait tout enseigner. Il enseigne les sciences naturelles, c’est le poste qu’il a réclamé, mais on lui fait aussi enseigner, au début, l’histoire et la géographie, la philosophie. Il enseigne à peu près tout.

Comme c’est un travailleur acharné, et qu’il ne faut pas se décourager, il veut reprendre des études. Là, la difficulté c’est que pour faire des études de sciences il faut un minimum de matériel, et dans son village il n’y a pas ça. Donc, il décide de prolonger en philosophie. C’est cela qui est peut-être le plus important, c’est l’irruption sur la scène de la philosophie française de quelqu’un qui n’était pas destiné à être philosophe, qui n’est pas un héritier, en aucun cas, d’une tradition lettrée, mais quelqu’un qui va profondément marquer, notamment par son travail d’enseignant en physique et en chimie, et quelqu’un qui a une tête bien faite d’un point de vue mathématique. Il passe en un an l’équivalent de nôtre master, puis il s’inscrit en thèse.

En thèse, il va être avec deux personnages, dont là je n’aurai pas vraiment le temps de vous parler, qui sont intéressants eux aussi : Léon Brunschvicg et Abel Rey. Léon Brunschvicg, en un mot, c’est ce qu’on appelle un néokantien, c’est-à-dire quelqu’un qui s’est beaucoup inspiré de la philosophie de Kant mais c’est surtout un bon connaisseur des mathématiques, quelqu’un qui fait des études justement d’histoire des idées philosophiques en fonction de l’évolution de l’histoire des sciences déjà, et un idéaliste. Abel Rey, c’est un personnage encore plus étonnant, c’est quelqu’un qui se revendique de quelque chose qui sert souvent de repoussoir de nos jours, il se dit « scientiste ». C’est lui qui revendique ce terme. Il s’inscrit dans le sillage du positivisme d’Auguste Comte mais il va encore plus loin. Quand on lit Abel Rey, se pose même la question de savoir, puisqu’il n’y a de vérité que des vérités scientifiques, ce qui reste à faire à la philosophie ? Bachelard a choisi les deux personnages d’avant-guerre qui pouvaient guider une personnalité comme la sienne pour travailler sur les sciences.

Il va soutenir deux thèses de philosophie en 1927. L’Essai sur la connaissance approchée, dont je dirai un mot, recevra un prix de l’Académie. C’est déjà une œuvre magistrale, qui traite essentiellement de la science qu’il a apprise durant ses études, autrement dit la science classique, la science du XIXe siècle. Il a commencé à s’initier à la théorie de la relativité, à la mécanique des quanta, mais pour l’instant, il n’aborde que des problèmes issus du XIXe siècle. S’il ne fallait retenir qu’une seule idée de l’Essai sur la connaissance approchée, c’est précisément l’idée d’approximation. Vous avez probablement un souvenir d’élève où on vous avait donné un problème de physique, vous aviez trouvé la bonne équation, vous aviez mis les valeurs des variables, puis vous aviez tapé à la calculette, obtenu le résultat, puis vous avez noté le résultat, vous étiez content de vous, et le prof passe, il raye le résultat et vous met zéro. Vous lui dite que c’est pourtant le résultat exact, il vous dit : oui, mais le résultat n’était signifiant que deux chiffres après la virgule, et vous, vous m’en avez mis cinq. Cela n’a aucun sens, vous avez oublié que vous étiez en train de faire de la physique, vous avez fait des maths. Car un chiffre exact n’a de valeur que mathématique. Toutes les sciences de la nature sont des approximations. Donc, c’est une réflexion très méthodique sur l’approximation du côté expérimental et sur l’approximation du côté mathématique. C’est extrêmement profond philosophiquement parce que cela veut dire qu’au lieu de chercher un monde idéal qui corresponde exactement à une idéalité mathématique, avec Bachelard on se rend compte qu’on cherche toujours à connaître les choses à une certaine précision, à une certaine échelle, à une certaine résolution, selon une certaine approximation du réel. Et c’est l’approximation qui est en fin de compte la réalité la plus relationnelle et la plus profonde. C’est une première rupture avec la métaphysique des philosophes : les conditions réelles de la connaissance sont à la source de ce qui peut être appelé « réalité », pas l’inverse.

Ce qui fait la valeur de Bachelard, seconde rupture, c’est qu’il ne s’en tient pas là. Une fois qu’il a fait ce travail déjà considérable, il se remet à travailler, en apprenant la science qui se fait à son époque. Il rencontre Langevin, il s’initie à la théorie de la relativité, etc. Il écrit, dès 1929, La valeur inductive de la relativité, qui est l’un des premiers livres sur les théories d’Einstein. Il y en a eu d’autres avant mais pas forcément aussi clairvoyant. Il va continuer. Il va aussi intégrer la mécanique ondulatoire de Louis de Broglie, la mécanique matricielle de Heisenberg, la physique quantique de son époque. Il va faire une synthèse en 1934, qui est Le nouvel esprit scientifique, où il définit les conditions nouvelles de la recherche et de la science contemporaine. C’est une œuvre dont les principes inspirent encore les recherches que je peux mener aujourd’hui quand j’essaye d’expliciter des recherches scientifiques, que cela soit au CERN ou en astrophysique. Les principes qui sont exposées dans Le nouvel esprit scientifique sont toujours féconds. Ils sont toujours utiles, je dirais même qu’ils sont rarement dominés par l’ensemble non seulement du grand public, mais même de certains de mes confrères qui utilisent des formes d’approche de la science qui parfois me semblent datées et périmées au regard de cet effort intellectuel qui a été fourni dès les années trente.

Je mentionne en 1936 un article qui s’appelle « Le surrationalisme », qui de nos jours est réédité dans un recueil posthume, « L’engament rationaliste », parce que Bachelard y présente sa démarche en faveur des sciences aussi comme « progressiste » au sens fort du terme. Dans cet article, le mot « surrationalisme », formé par analogie avec le surréalisme, signifie une sorte d’agressivité de la raison, de turbulence qui recherche la rupture, qui n’est pas du tout conservatrice, qui ne se satisfait pas d’une raison ratiocinante qui ne ferait que rappeler des évidences déjà acquises, des savoirs qui seraient finalement des habitudes de la mémoire plus que le fruit d’une recherche permanente de réforme de l’entendement. En 1936, c’est publié dans une éphémère revue, Inquisition, qui était en soutien au Front populaire. Ce texte affirme la convergence de la nouveauté qu’apporte le surréalisme en art, les doctrines nouvelles pour la science, la relativité, la mécanique quantique, et puis un certain socialisme. A vrai dire, le nouvel esprit scientifique, NES, c’est aussi pensé par analogie avec la NEP de Lénine, avec cet assouplissement du dogmatisme marxiste qui permit de faire respirer la société soviétique et de redémarrer. Il y a véritablement là un progressisme dont la pointe est cet article de 1936.

En 1938, il publie un livre, qui est encore beaucoup pratiqué dans l’enseignement secondaire, l’un des plus connu, La formation de l’esprit scientifique. Je le mentionne parce que c’est là-dedans que l’on va trouver l’une des clefs pour comprendre comment fonctionne le progrès selon Bachelard, c’est la notion d’obstacle épistémologique. En 1938, Bachelard a quitté le lycée, il a accepté de prendre un poste de professeur à Dijon. Il va enseigner d’abord les lettres, ensuite la philosophie. Sa femme est morte depuis un moment. Il élève seul sa fille, et c’est l’une des raisons pour laquelle il rechigne un petit peu à reprendre des responsabilités plus importantes, il reste en province. On va lui proposer un poste à Paris, il va le refuser. Finalement, il montera à Paris en 1940, à la mort d’Abel Rey qui avait été son maître. Il monte à Paris pendant l’occupation. La défaite de la France avait été un choc pour lui, c’est l’une des rares fois où l’on a un témoignage du fait qu’il vacille, qu’il n’est pas capable de faire cours. Pendant la guerre il va écrire, en 1940, un dernier travail d’épistémologue avec ses notes, La philosophie du non. Mais, pendant la guerre, l’information scientifique ne circule plus, donc il est sevré de ce qui l’abreuve pour travailler. Et il va initier, ou prolonger, parce qu’il avait fait quelques incursions auparavant, une ligne de recherche qui est très intéressante mais dont on ne parlera pas aujourd’hui, qui est sur l’imaginaire, la poésie. Le Bachelard le plus connu dans le monde, c’est plutôt ce Bachelard de la poétique des éléments ou de La Poétique de l’espace, c’est-à-dire cette ligne de réflexion sur l’autre moitié de la vie humaine, sur la nuit. Il y a la moitié diurne, celle de l’éveil, qui demande de la concentration, de l’application, de la rigueur, durant laquelle il faut refouler les images faciles et les facilités du langage, les séductions. Puis, il y a ce côté où en fait on se prête à l’imagination, à la rêverie, et c’est durant la guerre qu’il va beaucoup travailler là-dessus avec des livres comme : L’Eau et les rêves : Essai sur l’imagination de la matière, par exemple qui est très connu.

Après la Deuxième Guerre mondiale, en 1945, c’est déjà un vieux monsieur, et ses alliés philosophiques ont disparus. Bachelard dans les années 30, c’est quelqu‘un qui fréquente des Italiens, comme Federigo Enriques, des Suisses, comme Ferdinand Gonseth, qui a de jeunes admirateurs extrêmement talentueux, comme Jean Cavaillès, comme Albert Lautman, et tous ces gens vont disparaitre pendant la guerre (à part Gonseth) : Jean Cavaillès, parce qu’il était résistant, Lautman, parce qu’il était juif, Brunschvicg, dans la clandestinité, Enriques, etc. Donc, le milieu intellectuel dans lequel il évolue a disparu, la science, elle, a progressé. Qu’à cela ne tienne, il va se remettre à l’étude, racheter des manuels… Et, vous trouverez, dès 1949, dans Le rationalisme appliqué, Bachelard citant les travaux de Richard Feynman, ce qui est tout à fait stupéfiant, c’est une vitesse d’intégration inouïe. En général, il faut vingt ans, au minimum de décalage entre un travail scientifique majeur et son intégration. Ce qui suppose aussi que dans Bachelard on a parfois l’intégration conjecturale, spéculative, de travaux qui n’ont pas été prolongés ou ont été démentis ensuite. On trouve ce bouillonnement intellectuel de la science se faisant, avec des intuitions géniales et aussi des conjonctures aventureuses. Et il va y avoir un festival de trois livres extrêmement importants : Le rationalisme appliqué, où il va nous donner un diagramme du spectre de la philosophie des sciences, et où il va penser la notion de rupture. Puis, L’activité rationaliste de la physique contemporaine, et ça, c’est un livre fabuleux, immaitrisable, d’une richesse inouïe, dans lequel on trouve thématisée quelque chose qu’il met en œuvre depuis longtemps, qui est le concept de récurrence, dont je vais vous parler. Puis, en 1953, Le matérialisme rationnel, qui sera le dernier livre de philosophie scientifique de Gaston Bachelard. Ensuite, il va continuer d’écrire, on ne s’arrête pas comme ça de travailler, mais sera dans la veine poétique et imaginaire.

Il meurt en 1962. Il aura été consacré par l’admission à l’Académie des sciences morales, il aura refusé, parce qu’il se trouvait trop vieux, un poste au Collège de France. Il aura été interviewé à la télé, une interview qui restera longtemps le spectacle le plus suivi à l’ORTF. C’était une personnalité immensément respectée et en même temps populaire, une incarnation du meilleur de l’esprit de la IIIe République française.

Maintenant, on va parler de la notion de rupture. Pour mettre les choses un peu en place, on peut avoir l’impression, en première approximation, que c’est un dilemme assez facile, une contradiction assez facile entre l’idée de continuité et de discontinuité. Les choses sont un peu plus complexes que ça. Il faudrait pour bien faire parler de toute une série de gens, refixer des positions dans le champ philosophique. Comme on n’a guère le temps, on va juste regarder deux positions un peu extrêmes pour situer les choses.

Dans la première moitié du XIXe siècle, il y a quelqu’un qui a une extrême importance, c’est Auguste Comte. Auguste Comte, c’est la philosophie positiviste. C’est un modèle qui non seulement sera très influent parmi les penseurs qui s’intéressent aux sciences mais aussi parmi les scientifiques. Cela faisait partie, on va dire, de la culture de l’honnête homme que de connaître quelques rudiments de positivisme jusqu’à la Seconde Guerre mondiale. L’une des leçons les plus emblématiques de la doctrine d’Auguste Comte, c’est « la loi des trois états » qui affirme que l’humanité, quand elle rencontre des phénomènes surprenants, pour lesquels elle ne s’explique pas d’où ils viennent, passe par trois étapes, psychologiques et historiques. Le premier état c’est l’état religieux. La première façon de rationnaliser un phénomène comme le fait que la foudre tombe souvent sur le même arbre, eh bien c’est de dire « Zeus a maudit la nymphe qui est dans cet arbre », donc inventer une cause surnaturelle, personnalisée. C’est là, un premier motif de rationalisation.

Dans un deuxième temps, il y a un travail d’abstraction du langage, qui passe notamment par l’introduction de la logique, et c’est ce qu’Auguste Comte appelle l’état métaphysique. Dans le stade métaphysique, on cherche une explication à travers l’attribution d’une cause logique, à travers un parallélisme entre les mots qui s’enchaînent pour exprimer le phénomène et ce qui est présupposé comme étant l’enchaînement de la cause et des effets physiques. On va dire qu’il y a une substance qui attire la foudre dans l’arbre. Puis, vient un troisième stade, qui est l’état positif (« positif » n’est pas opposé à négatif, mais à fictif, positif cela veut dire réel). Le positivisme consiste à rationaliser les phénomènes sans en chercher les causes mais en cherchant la loi d’évolution des phénomènes. On ne s’intéresse plus à essentialiser la cause, on observe juste le phénomène, on en mesure l’évolution, et on trouve une loi mathématique qui décrit cette évolution, et peut donc la prédire aussi. Je simplifie mais c’est cela la base de la méthode positiviste, et à partir de là on ne peut qu’aller en avançant. Toutefois, toutes les sciences ne commencent pas au même moment et elles n’avancent pas au même rythme. On a commencé par l’arithmétique il y a très longtemps, ensuite la géométrie, puis les premiers travaux de statique avec Archimède, puis le début de la mécanique, où en plus de l’étendue on a rajouté les forces, puis ensuite on va rajouter des affinités et on aura la chimie. Après la chimie on va étudier la matière vivante. Puis, parmi les animaux, il y aura une espèce un peu particulière, qui est l’espèce humaine, à laquelle on consacrera la « sociologie », et celle-ci nous expliquera pourquoi justement les sciences se sont développées ainsi.

Voilà un modèle encyclopédique assez classique dont le continuisme est complexifié par ce décalage entre les sciences. Mais Auguste Comte accomplit deux ruptures pertinentes par rapport à la philosophie antérieure : premièrement, il observe que la science est devenue une tâche collective. On ne peut plus croire être capable, comme Descartes, de réengendrer toute la science tout seul. La science est collective et elle est aussi appliquée, c’est-à-dire que Comte reconnaît le rôle des ingénieurs dans le fait que la science permet une action, une information du monde. La seconde rupture, dont Bachelard va tirer profit, c’est que Comte observe aussi qu’il arrive un moment où les sciences changent de présentation et de mode d’initiation. Jusqu’au XVIIIe siècle, quand vous vouliez être un géomètre, on vous faisait lire les œuvres des mathématiciens antérieurs. Il y avait évidemment les éléments d’Euclide, ensuite Apollonius, Apollodore, les travaux de Cardan, etc. Puis, il arrive un moment où l’on écrit des manuels. Et c’est très important pour Auguste Comte qu’il y ait une transition entre ce qu’il appelle l’ordre « historique » des connaissances, l’ordre dans lequel les connaissances sont apparues, et l’ordre « dogmatique », c’est-à-dire l’ordre dans lequel on les apprend quand on a su les synthétiser et les mettre dans un ordre démonstratif et pédagogique. Le manuel signe cette forme d’accession à la maturité pour toutes les disciplines (on peut tous réfléchir au fait qu’il n’existera jamais de manuel de philosophie de ce type). Cette réorganisation de la connaissance au cours du passage entre l’ordre historique et l’ordre dogmatique, c’est quelque chose dont Bachelard se souviendra.

Voyez : ce modèle continuiste d’Auguste Comte, où un progrès procède par accumulation des faits positifs, il suppose quand même déjà des réorganisations, donc un certain nombre de ruptures. En fait il n’y a jamais eu de doctrine suffisamment bête pour présenter la science comme un long fleuve tranquille.

Puis, d’un autre côté, il y a Thomas Kuhn, qui publie La structure des révolutions scientifiques, en 1962, c’est-à-dire précisément l’année où meurt Bachelard. On reprochera d’ailleurs à Kuhn de ne pas avoir rendu à César ce qui est à César, c’est-à-dire de ne pas avoir parlé ni de Bachelard ni d’un autre chercheur, Ludwik Fleck, qui avait des idées assez proches des siennes. L’idée de Kuhn, est qu’on peut parler de progrès cumulatif seulement durant des phases limitées où les chercheurs travaillent au sein de ce qu’il appelle un « paradigme », ou avec un « paradigme » parce que ce terme est ambivalent. Ce qui signifie qu’il y a un certain motif, une certaine structure, souvent mathématique, qui sert à décoder et à expliquer certains phénomènes et ensuite peut être appliquer, par analogie, à plein d’autres phénomènes et qu’ainsi un savant essaye de tout faire rentrer dans un même système. Vous pouvez penser par exemple à toute l’importance qu’a eu la découverte de loi de la gravitation universelle par Newton et du fait qu’ensuite on a cherché à trouver des lois d’attraction pour expliquer tout, y compris les phénomènes économiques ou électromagnétiques. Cela a été un grand moment de paradigme newtonien, dans l’école française de physique en particulier, et cela a donné lieu à un raffinement de la physique extrêmement puissant dans certains domaines : la mécanique, la dynamique ; et cela a donné lieu également à des impasses, il a fallu à un moment donné sortir de ce paradigme pour expliquer l’électromagnétisme. Dans cette perspective, pour Kuhn, comme un scientifique travaille dans un paradigme, il n’est pas capable de voir les choses autrement. Donc, il utilise un seul paradigme, tant que cela marche tant mieux, il accumule, il raffine, il élabore mais il y a des choses qui ne rentrent pas ou ne sont pas traitable par son paradigme, ce qu’il appelle des anomalies. En fait il va y avoir des phases que Kuhn appelle les phases de science « normale », des phases où la science fonctionne dans un paradigme relativement stable, puis il y a un moment où la science devient instable parce qu’il y a de plus en plus de gens qui sont à l’extérieur du paradigme et qui disent que ce n’est pas comme cela que ça marche, et parce qu’ils arrivent à expliquer des choses que le premier paradigme n’arrive pas à faire. Et là peut se produire une révolution, pour résoudre les anomalies et pour d’autres raisons. Le point décisif, selon Kuhn, c’est que la décision de changer de paradigme n’est pas liée à un arbitrage objectif tel qu’on pourrait peser dans une balance en mettant un plus et un moins. S’il y a une révolution scientifique, c’est qu’un paradigme en supplante un autre, résolvant certaines anomalies mais pouvant aussi être moins performant sur d’autres points. Entre la théorie du phlogistique et la chimie de Lavoisier, il y a ainsi une véritable rupture et le modèle de Kuhn est extrêmement convainquant. Pour Kuhn, il ne peut pas exister un méta-paradigme qui nous expliquerait la raison pour laquelle un paradigme en supplante un autre. Chacun est enfermé avec ses lunettes, il y a une imitation des points de vue qui font qu’il y a des victoires, des révolutions qui se produisent. Il est inutile de prétendre que le second paradigme, s’il retrouve des résultats du premier ou s’il l’englobe, a sauvé le premier paradigme. Par exemple, au sujet du rapport entre Newton et Einstein, il observe que même si l’on retrouve des formules de Newton comme des approximations (quand la vitesse du mobile est faible devant celle de la lumière) dans la théorie einsteinienne, elles n’ont néanmoins plus le même sens. Donc, il n’y a pas de traduction possible, sinon cela serait le même paradigme.

Voilà donc une conception discontinuiste de l’évolution des sciences et du progrès, qui présente des ruptures très franches, des révolutions, les phases révolutionnaires, et qui est, pour fixer les idées, l’antithèse en quelque sorte du relatif continuisme d’Auguste Comte.

Maintenant, ce que l’on va voir avec Bachelard, c’est que ces deux solutions sont peut-être un peu trop simplistes parce que, quand on fait une rupture, on fait une rupture par rapport à quelque chose, et quand il y a une révolution, il y a peut-être quand même un progrès objectif quand un paradigme en remplace un autre. Une théorie peut en surpasser une autre en fournissant des éléments de comparaison, qui nous permettent de recréer une continuité du progrès à travers les ruptures. Pour cela, il faut adopter une espèce de moteur à trois temps. Comte a trois « état » mais une fois atteint l’état positif, la science fonctionne en régime continu. Kuhn dispose, lui, en quelque sorte, d’un moteur à deux temps : phase normale, phase révolutionnaire. Bachelard, nous propose une valse conceptuelle à trois temps.

Le premier concept, c’est l’obstacle épistémologique.

L’obstacle épistémologie, c’est extrêmement important méthodologiquement. Cela repose sur une hypothèse de Bachelard qui est l’homologie entre les progrès fait par un esprit humain au niveau individuel, pédagogique, et au niveau collectif, historique. Quand Bachelard parle de la « formation de l’esprit scientifique », c’est à la fois la formation des têtes blondes qui apprennent les rudiments des sciences, et l’Humanité qui progresse dans son organisation de la communauté scientifiques. Qu’on soit un étudiant ou un chercheur dans un domaine de pointe, ce que demande Bachelard, c’est de comprendre qu’on n’est pas en train d’accumuler dans un récipient vide. La tête de l’élève n’est pas vide, elle est déjà pleine d’images, pleine de mots, et celle du chercheur aussi, elle est déjà remplie de toute une série de choses que l’on va appeler les obstacles épistémologiques, qui sont des choses qui nous arrêtent de penser, des réponses toutes faites, des évidences. Et il faut se méfier des évidences, de nos certitudes. On commence toujours par se tromper, c’est l’idée de Bachelard. Corrélativement, et c’est une idée très profonde aussi, la définition de la vérité que donne Bachelard, ce n’est pas un point à l’infini vers lequel on tendrait, c’est la somme des corrections, des rectifications de nos erreurs. Ce que fait le progrès c’est rectifier ce que l’on pensait, parce qu’on commençait toujours par se tromper. Donc, la somme des corrections de nos erreurs, c’est cela la vérité, pour Bachelard.

L’obstacle épistémologique que je vais vous présenter, il l’évoque dans son autre thèse de 1927, où il traite de la théorisation de la propagation thermique dans les solides, et il rappelle, au début du livre, que jusque dans l’Encyclopédie de d’Alembert, Diderot et des grands savants de l’époque - subsiste une définition de la chaleur et de la propagation de la chaleur tout à fait surprenante : on pense alors que la chaleur se propage de façon radiale mais préférentiellement de façon ascensionnelle. Bachelard observe qu’il n’y a pas d’expérience bien conduite qui peut induire cette pensée. Et il y a même une expérience très simple qui la met en défaut. Si vous prenez une source de chaleur pour chauffer une barre verticale (et que vous empêchez l’air chaud de remonter), vous observerez que la propagation de chaleur se fait de façon parfaitement symétrique. C’était donc très facile de savoir que c’était faux, pourtant cela reste là jusqu’en 1779. Il y a ici une espèce de mystère. Dans La formation de l’esprit scientifique, Bachelard va faire toute une tératologie de l’esprit scientifique avec des gens très importants, comme Benjamin Franklin ou Gay-Lussac, qui écrivent des sottises, parce qu’ils laissent le langage penser à leur place. Ils laissent nombre d’images, parfois inconscientes, faire les réponses avant même d’avoir bien formulé la question. L’une des choses qui peut expliquer cette prégnance de l’évidence que le mouvement de la chaleur est radial puis ascensionnel, c’est un phénomène intime, totalement universel et d’une importance affective primordiale pour tous les êtres humains : le feu de cheminée. Un feu de cheminée, vous en avez besoin pour vivre ! La flamme, de toute évidence, cela vous chauffe et cela monte dans la cheminée, il n’y a aucun doute, c’est une source de cette évidence. Et cette image, Bachelard la retrouve dans un livre qu’il a publié en parallèle avec La formation de l’esprit scientifique, qui est La psychanalyse du feu, c’est-à-dire la psychanalyse de la connaissance objective du feu. Il faut analyser précisément toutes ces images parce que le feu est un phénomène si important, si crucial dans l’hominisation et dans la civilisation humaine, que son image fait objectivement obstacle à une étude rationnelle des phénomènes thermiques. Dans ses ouvrages qui traitent des images, Bachelard quitte le « nous » objectif de l’esprit scientifique et livre quelques confidence sur le « je » de son expérience intime. Ce n’est pas l’expérimentation, c’est l’expérience vécue. Là, il y a une image du père qui est extrêmement intéressante. C’est dans un chapitre qui est consacré au « complexe de Prométhée ». Il y a des complexes de l’esprit, qui ne sont pas forcément des complexes négatifs, il peut y avoir des nœuds qui servent à des sublimations positives, qui permettent justement de nous entraîner à un comportement rationnel, qui aliment notre attitude de recherche scientifique. Le complexe de Prométhée, c’est celui de la désobéissance adroite. Bachelard n’avait pas le droit d’allumer le feu, il a fallu qu’il attende d’être chez lui pour avoir le droit de faire le feu dans sa cheminée, c’était un privilège du père. Comme Prométhée qui a volé le feu, on apprend à faire un feu en désobéissant, en volant une boîte d’allumettes, en allant faire un feu dans la forêt. Il y a donc une transgression, mais cette transgression est adroite. Il n’est pas question d’être un incendiaire et de mettre le feu à la forêt. Il est question de savoir, de tester son aptitude à faire un feu en désobéissant à la règle mais en réussissant quelque chose d’adroit. Eh bien, c’est tout à fait ce que Bachelard pense être l’une des attitudes fondamentales d’un chercheur en science, cette capacité à désobéir à la règle par habilité pour produire quelque chose de nouveau et de flamboyant. Et cela nous amène au deuxième concept : la rupture.

L’expression « rupture épistémologique » ne se trouve pas mot pour mot chez Bachelard mais tout le monde l’emploie. Même si le mot rupture ne se trouve pas non plus au tout début de son œuvre, le concept est là depuis le départ. L’idée de Bachelard est que contrairement à une longue tradition de philosophie, notamment anglo-saxonne et empiriste, qui prétend que la science est un raffinement du sens commun, la science pense contre le sens commun. Le sens commun a toujours tort, même quand il a raison, parce qu’il aura raison par hasard et pas pour les bonnes raisons. C’est pourquoi il faut toujours rompre avec le sens commun pour dépasser les obstacles épistémologiques. Mais on ne se débarrasse jamais complètement des obstacles, la rupture, ce n’est pas une fois pour toute. Les obstacles épistémologiques, il y en a eu au début de la science, quand il a fallu expulser les métaphores et passer à l’état positif, comme aurait dit Comte, mais une fois que l’on est installée dans une théorie scientifique, de nouveaux obstacles apparaissent. Car les résultats de cette théorie peuvent sédimenter comme des évidences, comme un dogme, un absolu. La science devient elle-même un obstacle pour quand on se heurte à de nouveaux phénomènes. Il y aura, par exemple, un approfondissement dans les échelles d’expérience ou un nouveau formalisme beaucoup plus complexe, et certains refuseront ces nouveautés parce qu’elles ne correspondent plus avec les évidences qui sont devenues le sens commun savant. L’obstacle épistémologique est de nouveau là et la rupture est donc toujours cet effort nécessaire aussi bien pour l’élève, qui apprend les rudiments, que pour le savant, qui se situe à la pointe de la recherche.

Ce que détecte Bachelard, c’est que précisément le modèle positiviste, dans lequel on repère un phénomène déjà là, on le mesure et on construit une description mathématique, une loi, eh bien justement, il est insuffisamment pour comprendre la science en train de se faire au XXe siècle. La science ne fonctionne plus comme cela. C’est pour cela qu’il proclame une rupture vers un nouvel « état » : il prend le modèle positiviste, avec ses trois états, et y ajoute un quatrième, un « nouvel esprit scientifique », qui change les règles du jeu. La science ne décrit plus, elle construit les phénomènes. L’observation ne fait pas comprendre le vol, on n’a pas réussi à faire voler un plus lourd que l’air en battant des ailes. Regarder les oiseaux cela nous a donné le désir de voler mais cela ne nous a pas donné la clef pour voler, la technique, il a fallu justement avoir un tout autre mode de raisonnement et de conception technique pour arriver à voler. Pour continuer à filer la métaphore avec la combustion, prenons l’exemple de l’ampoule électrique d’Edison : tous les modes d’éclairage antérieurs reposaient sur la combustion, le fait de faire brûler quelque chose. Or le fil électrique, l’ampoule incandescente à filament, eh bien, c’est précisément une technique de « non-combustion », si le filament brûle cela n’éclaire plus. Donc, il n’y a pas de véritables progrès que par rupture, ce qui veut dire que l’esprit quitte les évidences pour reconstruire sur de nouvelles bases, en se donnant à soi-même son axiomatique, qu’il cesse de se fier à ses premières observations pour mieux reconstruire. Il faut bien reformuler le problème pour trouver les bonnes réponses. Après, il faut évidemment raffiner : il va y avoir de petites et de grandes ruptures. Il y a une révision permanente des connaissances à la marge et il y a aussi des ruptures fondamentales qui rejaillissent sur le point de départ du raisonnement, sur les bases axiomatiques de la théorie. Ce qui nous amène au troisième point.

Jusque-là, on pourrait penser que Bachelard n’a fait que devancer Kuhn, mais il introduit un troisième concept fondamental, celui de « récurrence » qui permet de comprendre comment le progrès des sciences se poursuit de rupture en rupture.

Qu’est-ce qui se passe quand on est dans la situation révolutionnaire que décrit Kuhn ? Son modèle est quand même extrêmement brutal. Est-ce la même chose quand on passe de la phlogistique à la chimie de Lavoisier ou de la mécanique galiléo-newtonienne à la théorie de la relativité restreinte ? Est-ce qu’il y a une rupture totale de continuité quand ce sont les bases du raisonnement, les axiomes qui sont remis en cause ? Je continue de prendre des exemples dans le domaine de chaleur. Là ou Kuhn dira Lavoisier remplace entièrement ce qui se faisait avant, Bachelard dit que c’est plus compliqué que ça. Si l’on regarde les travaux qui ont été fait il y a longtemps par quelqu’un comme Joseph Black, qui travaillait sur une doctrine qui s’appelait le calorique, elle paraît de nos jours complètement fausse. Il faisait partie des gens qui se heurtaient à l’obstacle épistémologique du substantialisme. Des gens qui s’imaginaient que la chaleur était une substance. Mais il chauffait de la même façon des corps différents, et il regardait jusqu’à quel point un corps « emmagasine de la chaleur » avant de commencer à fondre, de se détruire, d’irradier, etc. Il en conclut que tous les corps n’absorbent pas la même quantité calorifique. Il avait ainsi défini ce qu’on appelle la « capacité thermique massique » aujourd’hui, à l’époque on appelait cela la « chaleur spécifique », parce que c’est specific heat, en anglais. L’idée de Bachelard est, quand il y a une transformation scientifique, certains savoirs sont, probablement, définitivement, périmés. On peut les oublier, ils font partie du passé révolu de l’esprit scientifique. Mais d’autres savoirs qui étaient présents, restent là, sont sanctionnés, ils font partie de l’histoire sanctionnée. Ils restent dans le présent de l’esprit scientifique. Certaines expériences que l’on peut faire en pensant au principe de relativité avec Galilée ont eu lieu il y a très longtemps mais pour quelqu’un qui n’a pas encore appris cela, ce sont des choses neuves, ce sont des choses présentes, qui sont encore contemporaines. Il y a une différence entre la simultanéité des événements et la contemporanéité. Il y a des choses qui sont très anciennes dans le passé mais qui sont encore contemporaines au niveau de l’esprit scientifique. Il y a des choses qui sont simultanées maintenant mais qui sont des idioties et qui sont déjà périmées, au moment où la personne en parle, elle est déjà un vieil idiot. C’est assez fin parce que cela nous montre que le calorique nous a légué la notion de chaleur spécifique qui est encore valable alors que la phlogistique, on peut l’oublier, cela reposait sur l’idée qu’il y avait un fluide qui avait une masse négative. Si je voulais me faire l’avocat du diable, je dirais que de Stahl, puisque c’est de lui qu’il s’agit, a quand même légué un principe qui reste valable, il fut le premier a posé une équation chimique, le signe égal. Certes, il a mis dedans le phlogistique, et l’ontologie de Lavoisier va en faire table rase, mais le fait de dire que rien ne se crée, ni ne se détruit, c’est un principe de Stahl et il n’est pas faux, puisque Lavoisier l’a conservé. Vous voyez qu’en passant d’un paradigme à un autre tout n’est pas perdu, il y a des choses que l’on peut retrouver sanctionnées et les récupérer.

Ce principe de la récupération, Bachelard l’appelle « récurrence ». Par analogie avec la récurrence dans les mathématiques : quand on fait une démonstration, il y a des théorèmes de récurrence. Cela veut dire que si vous démonter qu’au stade zéro il y a quelque chose qui est vrai et qu’ensuite vous montrez que si c’est vrai au stade n cela sera vrai aussi au stade n+1, eh bien vous avez démontré que c’est vrai de zéro à l’infini, parce qu’on peut partir de zéro et chaque fois que l’on incrémente (1, 2, 3, etc.), c’est toujours vrai. Donc, la récurrence, pour Bachelard, c’est ce mouvement par lequel, quand on a fait un pas en avant, on se retourne et on voit mieux le passé, on l’éclaire mieux que le passé ne se comprenait lui-même. On récupère du passé ce qui est encore valable, on élimine le reste. Vous voyez pourquoi cela a un rapport avec ce que disait Auguste Comte à propos de l’ordre dogmatique qui n’est pas le même que l’ordre historique. On n’a pas découvert en premier les vérités premières, les vérités qui sont maintenant des axiomes.

Pour résumer, il y a l’obstacle, on se heurte à quelque chose sans même s’en rendre compte la plupart du temps. On doit s’abstraire et opérer une rupture, qui provoque une situation de crise parce que l’on perd ce que l’on avait bien établi, puis il y a, espérons-le, la récurrence qui transforme les normes scientifiques au nom même des valeurs qui avaient institué ces normes. Et cette dialectique de l’obstacle, de la rupture et ensuite de la récurrence, c’est le modèle du progrès chez Gaston Bachelard.

On voit la nécessité éducative de formuler une histoire récurrente, une histoire qu’on éclaire par la finalité du présent, une histoire qui part des certitudes du présent et découvre dans le passé les formations progressives de ses progrès.

Bachelard a aussi fait des travaux d’historien. Il n’ignore pas qu’il y a deux points de vue possibles. Il y a le point de vue que l’on est en train de décrire, ce point de vue récurrent, que les historiens appellent parfois « présentiste », parce qu’il juge du passé à la lumière du présent. Il y a un autre point de vue, que l’on pourrait dire « historiciste », parce qu’il se replace dans le référentiel historique d’origine. Le travail d’un bon historien des sciences est d’articuler ces deux points de vue. Si vous lisez certains livres d’histoire, vous trouverez des formules comme « il aurait dû savoir », et cet emploi du conditionnel qui se glisse sous la pointe avec un frisson d’uchronie, eh bien, c’est justement le point de vue présentiste qui éclaire subrepticement un point de vue historiciste. On présente l’état des connaissances à un moment donné, comment les gens se représentaient l’histoire et on dit : maintenant on sait que… On articule finement l’éclairage du passé par le présent avec l’idée aussi que parfois on doit justement comprendre, pour comprendre quels étaient les obstacles de ces gens, restituer ce qu’était le point de vue des acteurs en leur temps, qui est le point de vue des présentistes.

Le modèle bachelardien du progrès a un paradigme. Ce paradigme, c’est la découverte de la géométrie non-euclidienne. Dans La philosophie du non, le « non » vient de non-euclidien. Comment expliquer cela simplement ? Dans les éléments d’Euclide, on commence par une série d’axiomes, qui sont aussi des définitions, qui disent ce que c’est un point, une ligne, etc., qui sont autant de règles de construction. Mais il y en a une, le cinquième postulat, dont la formulation moderne est : « par un point extérieur à une droite, passe une et une seule parallèle ». Toutes les autres droites sont sécantes, mais celle-ci est non sécante à l’infini. La difficulté est que cela se présente un peu comme une définition, la définition de ce qu’est une parallèle, mais il y a une précision supplémentaire qui est : « une et une seule », et de cette précision il n’y a pas de démonstration. Donc, depuis l’Antiquité, il y a des gens qui se sont préoccupés de cela et qui ont essayé de démontrer le cinquième postulat d’Euclide. Parfois, ils ont cru y arriver parce qu’ils étaient partis, par exemple, de la somme des angles d’un triangle et qu’en fait ils se donnaient implicitement l’axiome à l’intérieur de ce qu’ils avaient choisi comme point de départ, donc ils le retrouvaient mais plutôt par analyse que par construction de concept. En fait, on n’y arrivait pas. C’était un vrai mystère et aussi, je dirais, un scandale parce que les éléments d’Euclide c’est précisément le modèle absolu du raisonnement a priori et rigoureux. À partir d’un certain moment, à la fin du XVIIe siècle, des géomètres vont essayer une démonstration par l’absurde. La démonstration par l’absurde, c’est tout simple : on va nier le postulat et on va en déduire les conséquences jusqu’à une contradiction flagrante et par conséquent on aura prouvé que le postulat est nécessairement vrai. Souvent, ils vont avoir l’impression d’y être parvenus, sauf qu’en réalité les contradictions auxquelles ils arrivent à exhiber sont des contradictions avec les résultats qu’on aurait obtenus si l’on avait admis le postulat. Par exemple, ils arrivent à la conclusion que la somme des angles d’un triangle n’est pas égale à 180°, donc c’est un problème. Mais en fait non, à l’intérieur de la logique de la démonstration il n’y avait pas de contradiction qui apparaissait. Le premier à se rendre compte que, du coup, on n’est pas en train de démontrer le cinquième postulat par l’absurde mais qu’on est en train de démontrer qu’une autre géométrie est possible, une géométrie non-euclidienne, c’est Lobatchewsky. Il était parti de l’idée que par un point on fait passer autant de droites non sécantes à une droite donnée. Il a mouliné et, à l’arrivée, il s’est rendu compte qu’il n’y avait aucune contradiction qui pointait à l’horizon, il a réalisé qu’en fait cela décrivait une nouvelle géométrie. Cela décrivait une géométrie hyperbolique. Sur une hyperbole, vous pouvez très bien imaginer un point et une droite, on n’appelle plus cela des droites mais des géodésiques, le plus court chemin pour aller d’un point vers un autre, on peut très bien imaginer ensuite un point distinct et des droites qui vont converger vers ce point puis divergent ensuite et qui ne se touchent qu’en ce point et qui ne sont pas sécantes à la première. Donc, il y a bien une infinité de droites non-sécantes et cela donne la géométrie hyperbolique.

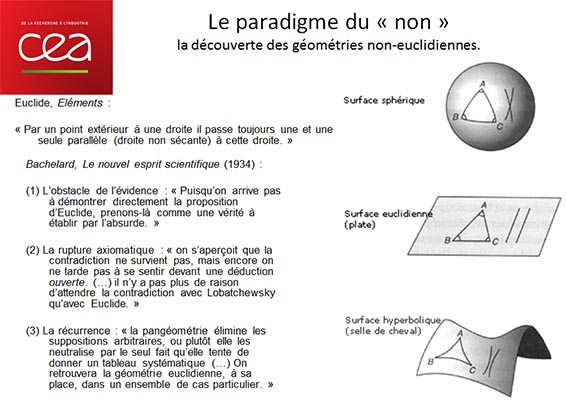
Le travail ne s’est pas arrêté là. Il y a eu les travaux de Poincaré et Felix Klein, qui ont démontré qu’axiomatiquement elles étaient équivalentes, il n’y avait pas plus de choses dans une géométrie que dans l’autre. Puis, il y a eu le travail du très grand mathématicien allemand Bernhard Riemann, qui a trouvé une autre forme de géométrie non-euclidienne, la forme, pour ainsi dire, symétrique de la géométrie de Lobatchewsky ; il a dit : par un point, je ne fais passer aucune parallèle. Et ça, cela vous donne la géométrie sphérique, parce que sur une sphère, la géodésique, l’équivalent d’une droite, est définie par deux points diamétralement opposés, c’est un grand cercle, comme l’équateur sur la terre. Quand vous prenez de grands cercles, ils se coupent tous, donc vous ne pouvez pas avoir de parallèles, les choses qui ne se coupent pas ce ne sont pas plus des grands cercles, ce sont des équivalents de segments. Riemann montre donc qu’il y a une autre géométrie non-euclidienne, mais en plus il invente le concept de variété, le concept de courbure. Il arrive à penser que toutes les géométries sont définies par une certaine structure mathématique, la variété, et se différencient suivant la courbure du plan que l’on considère, de l’espace que l’on considère. Par conséquent, il y a des géométries qui correspondent à des courbures positives ou à des courbures négatives, et il va y avoir comme cas très particulier, la géométrie plate. Et ce cas très particulier de la géométrie plate, c’est la géométrie d’Euclide, celle qui se fait sur un plan.

On vient d’assister à une vraie révolution conceptuelle. Si vous y réfléchissez bien, on a fait exactement ce que Bachelard décrit. On a d’abord eu un obstacle, l’obstacle de l’évidence. C’était une évidence que la géométrie euclidienne était juste, que c’était la seule, la vraie, c’était l’espace naturel. Kant croyait avoir démontré, dans La critique de la raison pure, que c’était la seule forme de la spatialité, la forme transcendantale extérieure. C’était tellement évident qu’on s’est dit que l’on va le démontrer par l’absurde, il suffit de nier cette évidence pour tomber sur une absurdité. C’était donc une certitude ancrée. Et quand on a commencé à avoir les premiers résultats les géomètres ont été effarés. Certains ont cru perdre la raison, d’autres ont dit : oh là, là, cachons cette géométrie bombée que je ne saurais voir… Il y a eu vraiment un moment de panique quand on s’est aperçu qu’il y avait une autre géométrie, indépendante, tout aussi efficace. A ce moment-là, c’était la panique parce qu’on a deux fondements de la raison. La pensée est toujours prise dans une tension, dans une certaine souffrance, quand elle est obligée de faire un raisonnement dialectique entre plusieurs bases.

Puis, par approfondissement, on est arrivé au moment de récurrence. On est arrivé au moment où non seulement ce la géométrie euclidienne n’était plus évidente, mais on ne pouvait même plus dire qu’elle était différentes des géométries non-euclidiennes. Tout appartient à un même ensemble et il y a un cas particulier, sur lequel on était tombé en premier parce que c’était le plus évident quand on traçait les figures dans le sable. Une fois que l’on a pris la géométrie non-euclidienne, on comprend mieux la géométrie euclidienne qu’Euclide lui-même. Vous comprenez bien aussi que du coup, cette refondation montre le simplisme de Kuhn. Ce n’est pas un paradigme qui a remplacé un autre, ce n’est pas le non-euclidienne qui a remplacé l’euclidien. C’est un approfondissement de l’esprit scientifique qui vient de s’opérer, la révolution, c’est réellement une révolution. C’est une refondation récurrente de la science.

Peut-être que cela ne se passe pas toujours aussi bien dans toutes les disciplines et tout le temps, mais Bachelard est au courant. Il nous dit qu’il y a quelquefois où l’on n’assiste pas à cela. Mais il dit : c’est avec ce paradigme-là qu’il faut penser les progrès décisifs qui ont été réalisés à partir de 1905, sous l’impulsion d’Einstein, et qui ont donnés la théorie de la relativité, la mécanique quantique. Dans l’exposé d’aujourd’hui, je n’irai pas beaucoup sur la mécanique quantique. On peut dire que pour la mécanique quantique, c’est beaucoup plus complexe, parce qu’on ne peut pas prétendre que la récurrence a eu lieu de façon parfaite. Mais dans la relativité en revanche, on a un cas de récurrence exemplaire.

C’est vraiment un exemple emblématique que la réception bachelardienne d’Einstein. Dans La philosophie du non, Bachelard commence par dire, il est tout à fait exact, et en ce sens Kuhn n’aura pas tort, que l’on ne peut pas traduire une théorie dans l’autre. On est bien obligé d’admettre qu’il y a une rupture, on n’obtient pas la relativité einsteinienne en compliquant la relativité newtonienne. En réalité, on est obligé d’abandonner la relativité newtonienne et ses fondements pour reconstruire autre chose qui est quelque chose d’immensément neuf. C’est une innovation radicale, de rupture. Il y a bien un argument qui est amené ensuite, vous voyez la récurrence s’enclenche et le mot récurrence n’est pas prononcé, c’est après coup, quand on s’est installé d’emblée dans la pensée relativiste que l’on retrouve dans les calculs de la relativité, par des mutilations et des abandons les résultats numériques fournis par l’astronomie newtonienne. Les astronomes traitent avec la relativité einsteinienne certains phénomènes mais il y a des cas où ils n’en ont pas besoin. Ils peuvent faire des pas mal de calculs avec les approximations newtoniennes suffisamment précises et qui simplifient les calculs. Pourquoi peut-on prendre cette décision pragmatique ? Parce qu’il y a beaucoup de cas où la vitesse de ce que l’on est en train d’observer est très faible par rapport à la lumière. Donc, il y a des termes qui deviennent négligeables dans les transformations de Lorentz (même si c’est Poincaré qui a donné la formule exacte). Si, pour mesurer la distance « x’ » après un certain temps « t », quand le mobile se déplace à vitesse « v » et qu’il est parti de la position « x », eh bien si la vitesse au carré, « v2 », est négligeable devant la vitesse de la lumière au carré, « c2 », un certain terme devient négligeable et on se retrouve avec une formule qui correspond, si l’on supprime carrément le terme, à la formule qu’on appliquait déjà avec Galilée. Mais ce que nous fait comprendre Bachelard, c’est que cela reste quand-même une mutilation, un abandon pragmatique. La complication, elle est bien là. On a décidé de ne pas la regarder, mais dans l’édifice théorique einsteinien, il n’y a pas la formule de Galilée. Donc, d’une certaine manière, il est d’accord avec Kuhn qui dit : « quand on retrouve une formule antérieure, elle n’a pas le même sens qu’autrefois ». Mais Bachelard ajoute : « oui, mais ce n’est pas cela qui est important, ce qui est important, c’est bien la reformulation de ce qu’avaient élaboré Galilée, Newton et les autres, car on comprend que leurs formules étaient des versions dégénérées, simplifiées, simplistes ». Ce n’est pas qu’ils étaient idiots, mais parce qu’ils étaient encore en train de regarder les phénomènes à une certaine échelle, avec certains instruments. En fait, avec la récurrence, on leur rend raison : ils ont fait l’effort de la raison. On les corrige au nom des mêmes valeurs que celles qui les ont poussées à élaborer cette formule. La relativité einsteinienne, c’est le moment où l’épistémologie de Bachelard démontre toute sa pertinence – le moment où sur la question théorique des ruptures, elle démontre sa supériorité par rapport au positivisme ou à l’incommensurabilisme de Kuhn.

Venons-en au présent. Je vous l’ai dit, je pense que l’épistémologie bachelardienne est toujours valable comme propédeutique pour aborder les problèmes actuels de la recherche, qu’elle reste toujours pertinente. Il y a beaucoup de penseurs qui feraient bien de prendre au sérieux les leçons d’épistémologie bachelardienne pour éviter d’arriver avec un esprit vieux, avec des concepts périmés, quand ils abordent les sciences. Par exemple, on ne devrait plus utiliser le modèle positiviste, avec sa description en langage mathématique de phénomènes mesurés préexistants, parce que la science contemporaine ne fonctionne plus du tout comme ça. Bachelard, lui, nous donne des clefs, en particulier dans Le Nouvel esprit scientifique et dans Le rationalisme applique.

Les deux concepts que je suis obligé de reprendre à Bachelard pour caractériser la science contemporaine sont « noumène » et « phénoménotechnique », deux termes qui peuvent paraître jargonneux mais qui ont le mérite d’inscrire dans la langue la nécessité de la rupture avec le sens commun. « noumène », c’est un vieux mot grec, que l’on trouve déjà chez Platon, mais que l’on doit comprendre par décalage avec la définition qu’en donnait Kant. Kant opposait les « noumènes  », en tant que « choses en soi », aux les phénomènes, les choses pour un sujet. Pour Kant, le sujet n’a affaire qu’aux phénomènes, dans l’espace et le temps, les « noumènes » sont inconnaissables. Dans les formes a priori de la sensibilité, le temps et l’espace, nous ne connaissons que des phénomènes. Nous ne pouvons faire d’expérience que des choses qui se présentent comme des phénomènes dans l’espace et dans le temps. Ce que sont les choses en soi, nous ne pouvons l’apprendre qu’à travers les phénomènes. Pour Kant, le seul « noumène » dont nous pouvons faire l’expérience, mais qui n’est pas une expérience scientifique, c’est notre liberté, mais cela n’a rien à voir avec le sujet. Donc, le « noumène » est inconnaissable, voilà ce que dit Kant : « Il n’y a de connaissance que des phénomènes ».

Que reprend Bachelard avec le terme « noumène » ? En mécanique quantique, on se rend compte que la structure mathématique de la théorie n’est pas du tout une « description » des phénomènes, c’est une structure mathématique qui induit et limite la possibilité d’actualiser certains phénomènes physiques. Il y a ce que Bachelard appelle une « valeur inductive » des mathématiques. L’un des plus beaux exemples, c’est la découverte de l’antimatière par Paul Dirac. En travaillant sur la mécanique quantique, ce mathématicien essayait de trouver un accord avec la relativité restreinte : que se passe-t-il si une particule quantique, un électron, se déplace à une vitesse proche de la lumière ? Oubliant pendant un moment ce que c’est qu’un électron et s’intéressant juste à l’équation de la propagation, il trouve un résultat et se dit à ce moment-là qu’il faut peut-être vérifier que cela correspond bien au cas de l’électron. Mais, en vérifiant que son équation marche avec un électron – c’était le cas, bravo ! – tout d’un coup il se rend compte que cela marche aussi avec une solution de signe inverse. Il se dit : mais qu’est-ce que c’est que cet électron avec une masse négative ? Je suis en train de retomber dans le phlogistique ! Qu’est-ce qu’une matière de masse négative ? Puis, il se dit : ah, c’est peut-être un trou au milieu de plein d’électrons, car si j’ai une mer d’électrons, un trou cela fait comme un truc positif au milieu d’un flux négatif. Puis, il se dit : mais non, ça n’a pas de masse, mais ça ne fait tout de même pas une masse négative ! Réfléchissant encore, il en arrive à penser qu’il doit exister une particule qui a la même masse que l’électron mais qui est de charge positive. Car la seule explication plausible de l’inversion du signe est la charge, pas la masse. Donc, un mathématicien se laissant seulement guider par ses équations conclut, sans aucune expérience concrète, qu’il faut qu’il existe un positon (ou positron, on dit les deux). Et deux ans plus tard, on obtient la création d’une paire particule-antiparticule.

L’équation de Dirac ce n’est pas une description en langage mathématique d’une observation. Il n’y a pas d’observation possible avant l’équation. Il a inventé, il a induit. C’est pour cela que Bachelard parle de valeur inductive. Cette valeur inductive, c’est comme une induction électromagnétique. Un aimant qui passe à travers une bobine induit un courant électrique. Un courant électrique induit un champ magnétique. Cela n’a rien à voir avec l’induction au sens de la logique. Bachelard montre que, dans la science contemporaine, les mathématiques sont une structuration de la réalité, ce sont des « noumènes ». Contrairement à ce que pensait Kant, ce qui est connaissable en mécanique quantique, c’est le noumène parce que c’est la structure mathématique de la théorie qui prescrit ce qui est observable. Les phénomènes, on les obtient comment ? On ne les obtient plus par des mesures sur des choses qui existent déjà, par des observations. On les obtient par des expérimentations, par des dispositifs expérimentaux qui créent le phénomène, qui sont des fabriques de phénomènes, comme on a eu la fabrique de la paire : particule-antiparticule. C’est pour cette raison que Bachelard forge le néologisme « phénoménotechnique » qui se comprend aussi par décalage. La « phénoménologie », c’est une description langagière des phénomènes pensés sur le modèle de la perception sensible, et Bachelard tient qu’elle ne sera plus jamais capable de rendre compte du travail scientifique, parce qu’on ne peut plus faire l’abstraction de la technique. Il y a un décentrement. Ce n’est pas le sujet perceptif, ce ne sont pas ses intuitions qui comptent. Il y a un décentrement à la fois à travers les mathématiques, qui rompent avec nos évidences premières, qui quittent la géométrie euclidienne, etc., et à travers les dispositifs phénoménotechniques qui créent les phénomènes, qui actualisent des potentialités que l’on avait jamais vu avant. À partir de ce qu’est prédit par la structure mathématique de la théorie, il y a cette induction de potentialité, et c’est cela que l’on quête dans la science contemporaine. Et ça, c’est encore vrai pour la quête du boson de Higgs au CERN dans le LHC.

Cette grosse machine, CMS, j’ai eu la chance de la visiter avant qu’on le ferme. C’est ce type de machine qui est nécessaire pour interagir avec le produit des collisions des faisceaux à très haute énergie : au cœur de ce détecteur, l’énergie cinétique des deux faisceaux de particules se transforme en une formidable énergie qui actualise des myriades de particules. Ces particules se désintègrent toutes très vite, il est hors de question de détecter directement un boson de Higgs, mais avec ses capteurs, répartis sur toutes ces couches différentes, ses trajectographes, ses calorimètres, etc., CMS recueille toute l’information possible sur les particules émises. On combine tout cela (en fait, on commence par éliminer 90% de l’information), puis on compare à des modèles statistiques (parce qu’on ne sait pas vraiment ce que l’on cherche). On sait qu’il faudrait un boson pour expliquer la masse de certaines particules, mais on n’a pas d’idée exacte de où il se situe lui-même en masse. Donc, on étudie tous les scénarios possibles, et deux ans plus tard, on voit sur la courbe une bosse. Et quand la bosse est assez haute, quand elle a 5σ, on dit : « ah, on a observé le boson de Higgs ! ». Et là, on retourne en arrière, on sort un cliché et on dit : « c’est la première fois qu’on a vu le boson de Higgs ». On n’a rien vu du tout ce jour-là ! Vous comprenez que l’observation est juste une déclaration à la fin, elle est entièrement rétrospective, entièrement récurrente. On n’est plus du tout dans la science positiviste du XIXe siècle où les observations précèdent le dégagement de lois grâce à une traduction mathématique. C’est même l’inverse ! Des modèles théoriques prédisent des virtualités qu’on essaye d’actualiser avec des dispositifs phénoménotechniques. Bien sûr, on souhaite aussi que la phénoménotechnique nous fasse découvrir des choses inexplicables et que la dialectique entre noumène et phénoménotechnique fonctionne dans les deux sens.

Certes, il y a des formes de scientificité différente maintenant, qui sont d’ailleurs souvent plus de la technologie, par exemple les nanotechnologies. Mais la phénoménotechnique serait quand même la porte d’entrée pour comprendre comment la raison s’y applique. Cela n’aurait peut-être plus la même portée de sublimation de la théorie.

Conclusions pour un philosophe qui s’intéresse aux sciences. Les mathématiques ne sont plus un langage de description mais bien la structure virtuelle dont on peut induire la possibilité de nouveaux phénomènes. On crée vraiment de la nouveauté, des phénomènes qui ont peut-être existé mais qu’on n’avait jamais observés à la surface de la terre, et qu’on ne pourrait jamais voir sans médiation technique. L’objet technique ne distord pas notre perception, il crée le phénomène. Il est notre unique moyen d’interagir avec ces échelles éloignées de la réalité. La technique n’est plus constituée seulement d’instruments de mesure appliqués aux phénomènes préexistants, mais d’instruments phénoménotechniques, de dispositifs de production de nouveaux phénomènes. En toute rigueur, il ne s’agit plus d’observer mais d’expérimenter.

La science du XXe siècle a opéré plusieurs ruptures d’échelle. La phénoménotechnique, ce sont toutes ces techniques qui interviennent, depuis l’échelle des molécules jusqu’à celle des particules élémentaires. Considérez que cela s’étend aussi aux grandes échelles parce que les messagers des structures à très grande échelle ce sont aussi des particules. Il y a bien des interactions avec la gravité, les ondes gravitationnelles qui sortaient mais cela demande aussi de la phénoménotechnique, le modèle n’est pas remis en cause pour autant.

J’arrive à ma conclusion. Les leçons que Bachelard a données peuvent servir au scientifique pour la compréhension de son propre travail, c’est une forme de réflexivité interne à l’esprit scientifique. Parfois, les scientifiques pensent à leur propre discipline avec une philosophie spontanée du savant, c’est-à-dire avec des outils philosophiques qu’ils ont appris eux-mêmes dans leur jeunesse, et ils sont en retard. Les philosophes étant en retard sur les scientifiques de leur temps, les outils sont très en retard sur ce qu’ils font eux-mêmes. Il n’est pas rare de voir encore des scientifiques penser mathématiquement de façon surationnaliste, c’est-à-dire être très en avance sur leur temps, à la pointe de la contemporanéité, et entendre les mêmes traduire dans un langage complètement archaïque, faux et mystifiant leur propres découvertes parce qu’ils ne disposent des concepts adéquats. Ainsi, il n’est pas rare d’entendre encore des scientifiques se référer à la méthode cartésienne, qu’il la connaisse ou pas d’ailleurs, alors que c’est le contraire de la méthode scientifique qu’ils emploient. La méthode cartésienne repose sur l’idée que l’on va faire ce doute hyperbolique, on va convoquer le malin génie, et quand on aura oublié tout ce que nos sens, le ouï-dire, etc., il nous restera quand même encore les mathématiques et puis là on va feindre qu’il existe un dieu mauvais pour nous dire que même les mathématiques sont fausses ; ça a l’air cohérent mais c’est une fable ; et à ce moment-là, résistera quand même quelque chose, un noyau de certitudes, un fondement absolu, cela sera le cogito : je pense donc je suis ; ce qui ne nous conduit pas bien loin, mais heureusement Dieu se ramène … Entendez bien qu’ici Dieu cela veut dire « conditions de possibilité de la connaissance », c’est normal que certains ecclésiastiques aient trouvé le Dieu de Descartes un peu douteux. Il assure : tout ce que tu penses avec les mathématiques, c’est vrai, tout ce que tu penseras à partir de ce moment en ayant choisi un point d’appui ferme et absolu qu’est le cogito, qui est une certitude, tu t’assureras de faire des transferts d’évidences bien solides, un peu comme dans une machine simple, on choisit un point d’accroche ensuite on a des poulies, on essaye de diminuer les frottements, on tire dessus, et tu vas produire une connaissance certaine : elle aura des racines métaphysiques et le tronc d’un arbre mathématique et les branches, ce seront la physique et les différentes sciences appliquées, l’optique, la médecine, les météores, etc. Et tout cela sera démontré une fois pour toute. On s’est soumis une fois au doute hyperbolique, et comme on a résisté, qu’on s’est purifié, on avance ! C’est peut-être le modèle le plus continu, mais ce n’est pas un modèle scientifique, c’est métaphysique. La science, ce n’est pas du tout comme cela que cela fonctionne !

La méthode scientifique est précisément une méthode non cartésienne. Car tout ce qui est une connaissance scientifique est révisable. La science ne peut pas avoir de dogme. Quand vous avez un problème, quand il y a une anomalie, la première chose est de vérifier que vous avez bien réalisé l’expérience. Puis, il faut vérifier que la méthode et le modèle que vous avez appliqués n’étaient pas faux. Si tout cela tient, il faut questionner la théorie, savoir si cela ne nécessite pas de la modifier. Puis, si cela tient encore, si vous n’arrivez toujours pas à résoudre le problème, il faut se demander si les bases de la théorie ne sont pas à remettre en cause. C’est ce qu’a fait Einstein. Il avait plusieurs raisons épistémologiques mais il y avait bien une anomalie avec le périhélie de Mercure avec l’expérience de Michelson-Morley sur la vitesse de la lumière qui était aberrante, il fallait résoudre un problème. Il y avait aussi et surtout le fait qu’il y avait une incompatibilité entre l’électromagnétisme et la mécanique. Toutes ces choses ensemble constituaient un faisceau d’anomalies. Einstein a fait quelque chose d’extraordinaire, il a remis en cause le fondement même de la connaissance qu’il avait apprise. Il n’y a que des génies qui opèrent des ruptures aussi profondes et trouvent des récurrences. Il n’a pas fait des ruptures en perdant le reste, pour cacher les problèmes. Il a fait une récurrence qui a englobé, qui a recréé tout l’horizon de ce que l’on a produit.

Vous sentez bien que le mot rupture suggère une forme de violence, ce n’est pas de la violence au sens physique bien évidemment, on est en plein dans la raison ; mais c’est la raison qui polémique avec elle-même ; c’est la violence de celui qui se fait violence pour prendre la bonne décision, pour rompre avec ses habitudes de pensée ; on peut même y voir une destruction créative, de l’innovation. Il faut bien détruire quelque chose pour construire quelque chose de neuf. « Toute découverte réelle détermine une méthode nouvelle. Elle doit ruiner une méthode préalable. » Cela veut dire que comme adversaire, si vous êtes un grand savant, un grand innovateur, un grand théoricien, un grand révolutionnaire, vous aurez les gens de votre métier, en tout cas un bon nombre qui ne voudront pas en démordre de ce qu’ils ont appris, de ce qu’ils tiennent pour vrai, de ce qu’ils ont construit comme évidence. Donc, il y aura une phase de combat parce que vous ruinez des certitudes auxquels vos collègues sont légitimement attachés. Si on rajoute une couche de Bourdieu, et il faut le faire, parce que Bachelard est au courant que la Cité scientifique est une organisation, c’est lui qui a nommé « l’union des travailleurs de la preuve », en comprenant qu’il y avait une organisation des institutions ; ce n’est pas désincarné la science de Bachelard ; donc il va bien y avoir des gens qui vont perdre tout leur capital symbolique, sauf s’ils se reforment, s’ils font l’effort de se remettre à l’école de la science nouvelle ; ce que Bachelard aura fait trois fois dans sa vie. Qui peut en dire autant ? « Dans le règne de la pensée, l’imprudence est une méthode. » Quand on vous dit d’être prudent en tant que chercheur, cela n’a pas de sens. Si vous manipulez un isotope dangereux, OK, mais ça, c’est pragmatique. Dans le règne de la pensée, non, soyez imprudents. Ne doutez pas de tout, tout le temps, ce n’est pas de ça qu’il s’agit. Osez douter des choses, même les plus fondamentales, c’est exigé par la vigilance épistémologique.
Justement, ce côté un peu aventureux, c’est quelque chose que Bachelard réfèrera souvent à Nietzsche, pas le Nietzsche de l’irrationalisme, mais un Nietzsche très rationaliste qui combat la raison par la raison ; Bachelard reprend à Nietzsche l’expression « tremblement de concepts », comme si la terre, le monde, les choses prenaient une autre structure du fait que l’on pose l’explication sur de nouvelles bases. Cela se trouve dans La dialectique philosophique des notions de la relativité, en 1949, autrement dit cela se trouve comme texte d’hommage pour le 75ème anniversaire d’Einstein, et Bachelard était le seul philosophe de langue française à être convié à cet évènement. En 1949, il n’est plus tout jeune.

Je termine sur le surrationalisme. « Il faut rendre à la raison humaine sa fonction de turbulence et d’agressivité. » C’est un message enthousiaste. Il n’y a pas de raison d’être, si on est authentiquement progressiste, sur des positions défensives. Il faut au contraire être fidèle à Gaston Bachelard, faire l’effort de venir à la rencontre de la science de notre temps, ne pas accepter les évidences, les idéologies. Je crois qu’à la prochaine séance vous aurez Françoise Combes, qui va vous parler d’un sujet qui n’est pas si neuf que cela, mais qui est toujours aussi controversé. De nos jours on a tendance, la plupart des scientifique, à prendre la matière noire pour l’hypothèse qui va de soi, et Françoise Combes, qui est professeure au Collège de France, elle, fait partie d’une famille de pensée qui dit : non, non, cela ne va pas du tout de soi qu’il faille accepter ce substantialisme, etc. Mais les résultats récents sur les ondes gravitationnelles remettent en cause l’hypothèse de la gravité modifiée qu’elle privilégie, donc elle doit elle-même se remettre en cause. Vous voyez que la raison polémique dont parlait Bachelard, ce n’est pas une vieillerie, cela existe toujours au présent. Il y a d’autres théoriciens qui sont engagés actuellement dans ces combats. C’est cela qui fait la vitalité, la turbulence et l’agressivité de la science contemporaine.

Je vous remercie pour votre écoute.

Anne Grange : Merci beaucoup pour ce brillant exposé. Je vais vous passer la parle. Si vous avez des questions, je vous demande de lever la main. Vous pouvez être turbulents mais pas agressifs.

Auditeur_1 : Bonjour ! Merci. Je voudrais juste, pour vérifier si j’ai bien compris, l’idée qu’il y a derrière le terme …

Vincent Bontems : Le concept.

Auditeur_1 : Voilà ! Finalement, c’est un peu l’idée qu’on ne valide pas un modèle parce qu’il permet d’expliquer mais parce qu’il permet de prédire et qu’on vérifie après.

Vincent Bontems : Je ne sais pas s’il faut opposer aussi nettement. Bachelard s’intéresse - on appelle cela des fois une épistémologie historique - aux phases de transformations des modèles. L’idée de la validation du modèle explicatif est aussi intéressante pour lui, il va beaucoup développer d’idées sur la vigilance épistémologique à l’intérieur du cerveau du chercheur quand il travaille à différents niveaux ; une espèce de récurrence interne, et qu’elle est homologue au fait de se présenter face à ses pairs. C’est-à-dire au fait qu’il y ait un jeu à la puissance multiple qui travaille dans le cerveau du chercheur, et qu’il travaille à différents étages, mais est-ce que la prédiction suffit ? La communauté scientifique correspond à une exigence qui est aussi d’expliquer. Cela dit, ce qui me passionne le plus, mon exposé était orienté sur l’idée de rupture et de progrès, ce sont les phases révolutionnaires – les phases de stabilité ne l’intéressent pas tant que ça, les phases d’adéquation des modèles n’intéressent pas Bachelard tant que ça – donc les moments où il y a des explications nouvelles qui entrent en jeu. Son insistance épistémologique porte plus là-dessus que sur un modèle de réfutabilité à la Popper. Après, ce que vous dites de la prédiction s’applique aussi à l’induction mathématique, il peut y avoir des phases où on neutralise la capacité du modèle à expliquer et on avance, pour ainsi dire, à l’aveuglette à l’intérieur des mathématiques, parce qu’on va neutraliser l’ontologie associée à un modèle, par exemple, et on va attendre de voir ce que cela donne avec les équations et ce que l’on peut observer. C’est le cas par exemple dans le très grand nombre de progrès qui ont été faits par transfert analogique d’équations d’un domaine à un autre, par analogie formelle. C’est le cas pour Einstein dans la mécanique quanta. Il prend une formule de thermodynamique, il la transfert au problème du corps noir, et c’est ça qui permet de faire émerger la constante de Planck. Dans ces cas-là, on se rend bien compte que le scientifique pendant un moment neutralise la capacité explicative, si j’ai bien compris ce que vous voulez dire par explication, parce que pour moi la capacité explicative, c’est quand on renvoie à une intuition de l’ontologie associé du phénomène qu’on est en train de modéliser. Mais peut-être que je me trompe et que ce n’est pas cela que vous vouliez dire. Si je me suis trompé, reformulez votre question. Dites-moi plutôt à quelle partie de l’exposé vous faisiez référence. Celui de la récurrence ?

Auditeur_1 : Non, non. C’était sur l’idée qui était cachée derrière … j’avais essayé de reformuler un peu ce que j’avais compris, pour vérifier que j’avais bien compris. Apparemment, non.

Vincent Bontems : Cela peut être un cas d’application, ce que vous dites. Pour qu’on parle sérieusement, il faudrait savoir où votre question s’applique. Dans Le rationalisme appliqué, Bachelard dit qu’il y a comme des régions sur lesquelles on applique sa raison. Il y a un rationalisme régional, dispatché, et cela ne correspond pas purement à une discipline. Il y a un rationalisme nucléaire, un rationalisme électronique … Il y a différentes phases où là se met en place un modèle et il y a une dialectique entre l’explication et la capacité de prédiction. C’est vrai que comme j’ai accentué le fait qu’il y ait un privilège du futur, parce qu’on essaye, quand on est surrationaliste, d’anticiper les ruptures qui vont arriver, peut être que c’est cela qui vous fait dire que la prédiction est plus forte que l’explication. Mais ce n’est pas tout à fait exact. En revanche, on pourrait voir ça dans ce cadre-là, dans Le rationalisme appliqué. Il faudrait prendre des exemples parce qu’on ne peut pas parler en l’air des concepts, il faut les appliquer sur un cas.

Auditeur_2 : Bonjour ! Des fois, les gens ne savent pas prendre le virage, pour faire une belle découverte. Je citerais le cas d’Henri Moissan, Prix Nobel pour avoir isolé le premier le fluor, qui écrivait cependant la formule de l’eau HO, ce qui a traîné pendant longtemps.

Vincent Bontems : Oui, bien sûr, il y a tous ces phénomènes d’erreurs et de résistance mais ce qui est beau dans la science, c’est que parfois les scientifiques sont amenés à admettre les découvertes à leur cœur défendant. Vous savez pourquoi la constante de Planck s’appelle h ? À cause de Hilfe, qui veut dire « au secours » en allemand. Planck était un partisan de l’énergétisme et du continuisme absolu de la matière. Quand il est tombé sur sa constante, il n’était pas content du tout ! Il était persuadé qu’il avait fait une erreur, ensuite il était persuadé qu’on trouverait une solution. Et quand est venu lui rendre visite en lui disant : « Vous êtes un génie, vous méritez le prix Nobel pour avoir trouvé ça … » Il a dit : « Non, non, c’est la pire chose que j’ai faite dans ma vie. » Et pourtant il a amené une contribution tout à fait majeure et une rupture essentielle dans l’histoire des sciences.

Auditeur_2 : Un petit point de détail. L’administration que vous avez appelée P&T, pour Gaston Bachelard, s’appelait à l’époque PTT, elle ne s’est appelée P&T qu’en 1925 pour une vingtaine d’années.

Vincent Bontems : J’en doute, mais je vérifierai. Quand on est bachelardien, il faut toujours accepter les corrections. Je vérifierai parce que je me suis peut-être fié à une information de seconde main. Pour moi, il a fait partie des Postes et Télégraphes, vous n’avez forcément pas tort parce qu’il connecté les fils de téléphone juste avant la Première Guerre mondiale.

Auditeur_3 : Bonsoir Monsieur ! Merci pour votre exposé, passionnant. J’ai une question au regard des découvertes purement récentes, je voudrais notamment faire allusion au théorème de Fermat, où finalement on a mis je crois plus d’un siècle pour démontrer ce théorème, à partir finalement, comme vous l’avez mentionné, d’objets mathématiques qui ont été finalement mis au point plus tard. Je vais rebondir là-dessus parce qu’aujourd’hui on a, il me semble, 7 problèmes mathématiques mondiaux qui ne sont pas encore résolus. Je pense notamment à la turbulence sur laquelle j’ai travaillée et à laquelle je me suis intéressée, où l’on n’a pas les outils mathématiques, parce qu’on a à faire à des équations extrêmement compliquées. D’après vous, est-ce que scientifiquement le fait de tenter de démontrer un nouveau postulat, un nouveau théorème, ou un nouveau phénomène, va induire une autre approche des mathématiques, qui sont aujourd’hui inconnues ? Comment vous expliqueriez et comment vous voyez cet aspect-là ? Je pense notamment à ces deux aspects de Fermat, où on a été obligé de mettre au point de nouveaux principes mathématiques. Peut-être que d’autres approches mathématiques au regard de la turbulence, par exemple. Merci.

Vincent Bontems : Oui, il peut y avoir une approche en mathématique qui a des affinités avec le bachelardisme pour avoir recours à une forme particulière de récurrence. Je me risque rarement à en parler, pour une raison simple, c’est que les mathématiques sont le domaine le plus puissant. C’est l’endroit où il y a le paysage le plus vaste et le plus varié de conception possible. Sur le théorème de Fermat, il faudrait demander l’avis d’un mathématicien historien. L’idée est, je crois, que Fermat n’avait pas la démonstration en tête quand il l’a dit, il croyait l’avoir (ou il a fait une blague), mais la complexité de la preuve par Wiles montre qu’elle était inaccessible à son époque. Ce que vous dites, c’est très juste mais comme vous le reliez au domaine des turbulences la question est de savoir est-ce que cette stratégie purement interne aux mathématiques peut résoudre un problème de physique. Souvent les mathématiques ont engendré des outils apparemment inutiles qui ont été retrouvés plus tard par les physiciens. C’est un champ très, très vaste, je me suis un peu intéressé à des problèmes de turbulence qui ne sont pas forcément analogues, et c’est clairement des domaines où il faut être compétent. En gros, je ne peux même pas commencer à répondre à votre question, seulement à la comprendre, si nous travaillons ensemble à la reformuler. Il me faut un informateur, je ne suis pas assez comptent. Aujourd’hui, de toute évidence, ce que je vous ai donné comme épure, c’est un modèle qui, même si son paradigme c’est la généralisation de la géométrie non-euclidienne, demeure dans l’horizon d’attente de ce que doit être une théorie physique. Je ne sais pas jusqu’à quel point cela correspondrait à ce dont on est en train de parler, à propos des turbulences.

Désolée de ne pas pouvoir répondre mieux.

Auditrice_4 : Est-ce qu’on peut considérer comme des ruptures scientifiques, premièrement le théorème d’incertitudes de Gödel et deuxièmement la théorie du chaos ?

Vincent Bontems : Cela va être oui et peut-être. Oui, le théorème de Gödel, c’est absolument certain que c’est une rupture fondamentale et c’est très en affinité avec ce qu’on vient de voir. Le théorème de Gödel a cela de fabuleux qu’il met un terme au fantasme de l’auto-fondation absolue du système du savoir en même temps qu’il crée cette idée d’une connaissance toujours lacunaire, avec des énoncés indécidables. Le théorème de Gödel signe donc l’arrêt de mort d’une direction de pensée fondationiste : trouver un fondement absolu à partir duquel on pourrait tout démontrer … un néo-cartésianisme plutôt qu’un non cartésianisme. Ce n’est pas un hasard si la famille de pensée à laquelle appartient Bachelard et les gens que j’ai cités sont sceptiques vis-à-vis des programmes fondationistes et en particulier celui en mathématiques de Hilbert, ou vis-à-vis des néo-positivistes du Cercle de Vienne, qui propose un programme logiciste qui est tout aussi fondationiste. Il y a une très claire conscience chez Bachelard, Enriques, Gonseth, Cavaillès, qu’en science il n’y a pas de fondement absolu. La science se fonde en quelque sorte dans son mouvement vers l’avant et elle n’a pas à chercher un ensemble de certitudes stables et absolument consistantes. Si bien qu’un état d’incomplétudes, pour reprendre une analogie avec le théorème de Gödel, est l’état normal et préférable de la connaissance.

Je dirais qu’en plus de ça, il y a un travail de réforme de la logique, de la compréhension de ce que c’est que la logique, qui se prolonge dans les travaux de Paul Cohen sur le forcing, la démonstration de l’indépendance de l’axiome du continu, etc. Et toutes ces choses-là, participent du même horizon de pensée que la révolution du nouvel esprit scientifique. Oui, il y a une très grande affinité entre le théorème de Gödel et ce qu’on vient d’exposer. Il y aurait pleine de ramifications à exposer.

Sur la théorie du chaos, cela dépend de ce que vous mettez derrière cette appellation. C’est un terme qui apparaît je crois avec David Ruelle, et il y a plein d’autres termes qui apparaissent, qui sont très populaires et assez mal définis, comme « l’effet papillon », qui vient de Lorenz. Donc il faudrait préciser de quoi en parle pour essayer de délimiter la portée épistémologique et scientifique de ces travaux. Il est certain qu’il y a toute une série de choses qui sont faites dans les travaux de Poincaré sur les homoclines qui sont maintenant récupérées, je dirais de façon récurrente, rétrospective, par ce que l’on appelle la théorie du chaos. Il y a tout ce fond du domaine du chaos déterministe qui intéressait déjà Bachelard à son époque, même s’il ne connaissait pas cette expression. C’est dans le livre qui s’appelle L’activité rationaliste de la physique contemporaine. Il y a un assez beau chapitre qui commence par étudier un peu ce problème avant de poser des questions qui sont liées plus à la physique des particules. Donc, là, une fois de plus, c’est compliqué, cela me demanderait de travailler et je ne pourrais pas répondre en 5 minutes. Mais c’est une bonne question. La preuve, c’est que je ne peux pas y répondre, un peu comme la question du Monsieur sur la turbulence.

Auditrice_5 : Je voudrais revenir sur l’idée de progrès dans les paradigmes. En fait j’ai du mal à voir comment on peut vraiment parler de progrès alors qu’il n’y a pas de méta-paradigmes qui puissent juger objectivement l’idée de progrès parmi tous les paradigmes.

Vincent Bontems : Cela vient du fait qu’il faut remettre en cause finalement l’idée de Kuhn qu’il n’y a de progrès qu’au sein d’un paradigme fermé. En réalité, la recherche est à la fois plus souple, plus complexe, plus dialectique, et plus ouverte que ça. Dans la mesure où quand un chercheur cherche, il peut neutraliser tout ou partie de son … plutôt que paradigme, je vais prendre le terme de concept qui correspond mieux à ce que dit Bachelard. Donc il peut se situer ordinairement dans un référentiel théorique donné et avoir à un moment donné un référentiel de travail où il relâche, par exemple, tel ou tel des axiomes qu’il accepte en règle générale, il relâche des contraintes pour voir ce que cela fait. Autrement dit, ce que Kuhn dit à propos de la fermeture des paradigmes, c’est assez primitif par rapport au travail concret du scientifique, qui peut très bien transformer son référentiel, et qui, plus que ça, peut très bien se former en permanence un horizon d’ouverture, c’est-à-dire savoir que son référentiel est en état d’incomplétude et attendre justement l’information qui permettrait de changer de référentiel ou de savoir quelle partie de son référentiel il doit abandonner. Après, est-ce qu’on a vraiment besoin d’un méta-référentiel qui domine tout cela pour parler de progrès ? La réponse est non. On travaille dans l’histoire. Pour me moquer un peu de Kuhn, il y a un de ses élèves, Errol Morris, qui raconte une histoire qui s’appelle L’histoire du cendrier. Il disait : « Je suivais les cours de Kuhn, et je ne comprenais pas sa certitude sur l’incommensurabilité des paradigmes, puis à un moment donné je l’ai interrompu et j’ai dit : il y a des paradigmes qui se succèdent, sans qu’on puisse jamais les comparer, et puis il y a Kuhn qui prend la place de Dieu pour décider qui est-ce qui gagne ». Kuhn fumait cigarette sur cigarette. Il a été si énervé par la remarque qu’il lui a balancé le cendrier à la figure. Ce qui l’a énervé, c’est que l’étudiant souligne que le refus de toute commensurabilité entre différents paradigmes était un dogme qui permettait d’asseoir son autorité plutôt qu’une hypothèse dont on pouvait étudier la validité. Dans l’idée qu’on aurait besoin d’un méta-paradigme se cache une exigence qui est impossible à satisfaire parce qu’elle n’est pas justifiée : finalement on se met dans une position de surplomb quasi divine, on ne cherche plus une fondation absolue mais un surplomb absolu qui nous permettrait d’arbitrer. Or cela ne se passe jamais comme ça. Cela passe précisément par les mécanismes de formation de référentiels qui eux vont avoir d’une part un domaine d’intelligibilité, une extension, une validité, une précision particulière et, d’autre part, une capacité d’expliquer les référentiels antérieurs par la récurrence. L’esprit scientifique comporte cette partie réflexive que Bachelard a analysée. Pour répondre à Kuhn, on a besoin en fait de répondre à Abel Rey. Abel Rey disait : « maintenant, la science fait tout et elle interprète elle-même sa propre histoire, par conséquent il n’y a plus de place pour la philosophie ». Kuhn dit quelque chose d’analogue mais discontinuiste, il dit qu’il n’y a que des paradigmes fermés, comme des bulles de savon, et qu’il n’y a pas d’interprétation de toutes ces bulles qui se succèdent. Ce que dit Bachelard, c’est qu’au contraire il y a des gestes philosophiques qui sont de tout temps (pas tout le temps !) à l’œuvre dans la science, et qui précisément sont ces changements de référentiels, où l’esprit scientifique est capable de voir dans son passé ce qui est périmé, ce qui est sanctionné, et quel est l’horizon surrationaliste d’ouverture vers le futur. Il n’y a donc pas un paradigme unique à un moment donné mais bien plusieurs référentiels capables de se transformer et de chercher des récurrences. Il y a des sous-référentiels qui sont des modifications, obtenus même par mutilations et abandons, on peut retrouver dans le présent des strates passées. Et grâce à l’attente surrationaliste de futures révolutions, on peut déjà commencer à douter du référentiel-paradigme dans lequel on se trouve. Ce qui important pour la philosophie des sciences ce n’est pas d’inventer un méta-référentiel qui jugerait tout cela d’un point en dehors de l’histoire, en surplomb, c’est de trouver une façon toujours plus juste de décrire les transformations entre les référentiels.

Donc, pour répondre à votre question, il faut sortir de la formulation du problème par Kuhn. Il nous dit : « on ne peut pas traduire le concept d’un paradigme dans un autre paradigme, donc ils sont incommensurables ». Déjà il a une idée de la traduction qui est bête ! Il faudrait selon lui trouver une correspondance terme à terme, or ce n’est pas cela la traduction. Toute personne qui fait une traduction sait qu’il faut prendre un ensemble de relations et essayer de retrouver un autre ensemble de relations et non pas une équivalence terme-à-terme. Et, même si on lui accordait l’incommensurabilité des paradigmes, il faut justement comprendre comment celle-ci se crée historiquement : il y a des phénomènes de commensuration et d’incommensuration. Il y a des moments où les paradigmes divergent jusqu’à devenir incommensurables, en même temps que d’autres efforts de l’esprit scientifique qui sont précisément des commensurations. Comment repenser à ce que pensait Euclide à son époque, repenser à ce que pensait Galilée à son époque, à la lumière d’aujourd’hui, comment trouver ces articulations entre le passé et le présent, entre l’historicisme et la récurrence, le présentisme. Voilà le vrai travail.

Auditeur_6 : Merci ! Bonsoir ! Depuis l’Antiquité, les philosophes grecs se posaient des questions sur ce qu’est la réalité. Cette question a à peu près disparue jusqu’à la fin du XIX-XXe siècle, et elle revient, pas seulement en question philosophique mais aussi en question physique, par l’apparition de la physique quantique. Et cela continue jusqu’à aujourd’hui où on la traite dans les laboratoires pour comprendre ce qu’est la réalité. Il y a des expériences pour comprendre ce qu’est la réalité et découvrir d’autres dimensions qu’on ne connaît pas. Bachelard, qui a bien sûr connu le début de la physique quantique, quelle était sa conception et comment il a vécu ce débat qu’il y a eu entre Bohr et Einstein et les implications philosophiques de la physique quantique ?

Vincent Bontems : Je ne vais pas pouvoir répondre en entier à la question parce qu’on n’a pas le temps. Il faut y passer une année de séminaire. Je vais d’abord traduire. L’une des tâches de la philosophie rationaliste, c’est d’essayer, parce qu’elle prend la science de son temps en considération, d’expliquer comment on connaît et pourquoi on connaît ce qu’on connaît. C’est une théorie de la connaissance. La plupart des philosophies ont une traduction ontologique, elles prononcent un discours sur l’être. La question est de savoir jusqu’à quel point la tension entre ce qu’elles ont compris de comment on connaît ce qu’on connaît et la traduction, souvent dans un langage substantialiste, de ces connaissances en ce qu’elles sont, est féconde. Je contredirais volontiers votre appréciation, je pense que cela a eu lieu assez largement dans l’histoire, cette discussion : on trouve des interrogations pas seulement à partir du XIXe siècle. Mais c’est vrai qu’il y a un point d’acuité qui vient du fait qu’à partir de la révolution du 1905, il y a des phénomènes nouveaux qui apparaissent et notamment il y a une remise en cause radicale des traductions substantialistes, parce qu’on arrive plus à fixer un corrélat ontologique des modèles quantiques, que j’ai un peu évoqué avec l’histoire du « noumène » et de la phénoménotechnique. Il peut y avoir divergence d’actualisation soit sous forme d’ondes soit sous formes de particules, par exemple. Or ce n’est pas une situation accidentelle, c’est la théorie qui déclare impossible cette traduction – on pourrait analyser ici des implications fondamentales du théorème de Kochen-Specker. Il y a donc une crise du substantialisme extrêmement profonde qui implique de redéfinir la « réalité ». Comment Bachelard y répond ? D’une part par cette articulation entre « noumène » et phénomène. D’autre part, en soulignant que la « réalité », ce n’est pas possible à traduire de façon substantialiste, la réalité, elle est à traduire dans les relations. « Au commencement était la relation », disait-il. Donc, il y a un réalisme après le substantialisme, un réalisme des relations, qui fait qu’on n’est pas tenu de donner une ontologie sous la forme périmée des métaphysiques qui se sont effondrées au début du XXe siècle. Les structures mathématiques méritent d’être interprétées aussi à un certains stade plus fondamental, ce n’est pas simplement qu’on revient vers des observables, qui sont celles d’une onde ou d’une particule qu’on commence le discours, on peut se poser des questions pour savoir quel est le corrélat ontologique d’une fonction d’onde ou d’un espace des phases. Bachelard s’y est risqué dans un livre qui s’appelait L’expérience de l’espace dans la physique contemporaine. La piste qu’il suit c’était de revenir sur l’attribution d’une localisation parfaite à un corrélat ontologique : avec la formulation de la mécanique quantique par Heisenberg, celle de la mécanique matricielle, on peut toujours parler des étants mais ils ne sont plus strictement localisés. Son ami Gonseth allait encore plus loin. Il disait que la logique finalement c’est la physique de l’objet quelconque. Une fois qu’on a enlevé toutes les déterminations physiques, il reste une forme creuse, qui est celle de la logique, avec des principes de non-contradiction, d’existence et du tiers-exclu, etc. Cette logique porte en elle une ontologie en creux, une ontologie substantialiste qui fait qu’on pense qu’il existe des choses avec des propriétés comme on parle d’un terme auquel on attribue un prédicat. Avec Bachelard, ils ont convenu que la mécanique quantique précisément n’est pas une mécanique de l’objet quelconque. Donc, la logique et son substantialisme inhérent devrait être assouplie ou devrait prendre des formes postgödeliennes. C’est une logique différente qui s’applique à la mécanique quantique quand une particule est dans un état superposé. Donc, il y aurait une piste pour aller chercher un rétablissement de l’ontologie au XXe siècle à travers une réforme de nos schèmes, à condition de se situer dans un réalisme des relations, en instituant plutôt un prima de la relation sur les termes de la relation. Il n’est pas exclu que Bachelard ait avancé des pistes pertinentes dans ce domaine que vous appelez « comprendre ce que c’est que la réalité ». Par ailleurs, cela amène à beaucoup de prudence. Car les physiciens ne sont plus d’accord entre eux sur les interprétations. Il y a eu des débats entre Bohr et Einstein mais aussi avec Schrödinger, Heisenberg, Pauli, Majorana, etc. Tous les pionniers ont eu leurs propres tentatives de rationalisation. Au bout d’un moment le débat s’est un peu tari, et surtout on est arrivé à des stratégies pragmatiques : « shut up and calculate », on a mis tous ces problèmes sous le tapis, et on a continué la construction mathématique à travers la théorie des champs, etc. C’est donc de vieux problèmes jamais résolus et il faut savoir à quel moment de l’histoire on est en train de se placer pour discuter sérieusement votre question. Et cela prendrait des heures ! Comme les précédentes questions !

Anne Grange : On n’a pas des heures devant nous… On est obligé de s’arrêter là pour ce soir. Merci beaucoup pour cette passionnante introduction à ce cycle.

Vincent Bontems : Je vous remercie tous d’être venus.